Skip to content


Two most basic steps are required in ensuring that a numerical model works for predicting evolution and inundation. While the first step is ensuring that the model conserves mass, the second basic step is checking convergence of the numerical code to a certain asymptotic limit.

Mass Conservation

The conservation of mass equation is part of the equations of motion that are solved in any numerical procedure, but cumulative numerical approximations can sometimes produce results that violate mass conservation. This is particularly the case when friction factors are used, or smoothing to stabilize inundation computations for breaking waves.

Conservation of mass can be checked by calculating the water volume at the beginning and at the end of the computation. This should be done by integrating disturbed water depth $\eta (x,y,t)$ over the entire flow domain, i.e., if the flow domain extends from the maximum penetration during inundation $x=X_{max}$ to the outer location of the source region $X_{S}$, and $y=Y_{max}$ to $Y_{S}$, then total displaced volume $V(t)$ is


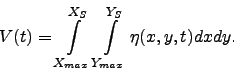\begin{displaymath} V(t)=\int\limits_{X_{max}}^{X_{S}}\int\limits_{Y_{max}}^{Y_{S}}\eta (x,y,t)dxdy. \end{displaymath} (1)

The integral of $\eta (x,y,t)$ should be used instead of the integral of the entire flow depth $h(x,y,t)=\eta (x,y,t)+d(x,y,t)$--where $d(x,y,t)$ is the undisturbed water depth--because the latter is likely to conceal errors in the calculation. Typically, $\eta \ll d$ at offshore integrating $h$ will simply produce the entire volume of the flow domain and will mask errors. Note that testing of the conservation of mass as above involves placing a closed domain within reflective boundaries.

Numerical models use absorbing boundaries to allow the wave to radiate outwards. While some loss of mass may in theory occur due to the differencing at the boundary, placing the computational boundaries far enough from the source ensures this loss is minimal. Nonetheless, testing conservation of mass with open boundaries and monitoring the volume fluxes over the corresponding boundaries at $x=x_{b}$ and $y=y_{b}$ is computationally possible. The net flux needs to be added or subtracted to the total displaced volume.

The calculation of the entire volume of the wave motion of the flow domain at the beginning and end of the computation--to ensure that mass is conserved--is very important in code validation. Once the associated mass fluxes at the boundaries are considered, numerical errors can be highly additive, and mass invariably decreases in numerical computations. It is essential that codes self-monitor the entire volume; if the difference between start and finish is greater than $5\%$, the grid needs to be readjusted. Usually with few changes in $\Delta x,$ $\Delta y$, and $\Delta t$, the conservation of mass can be improved.

Calculations of conservation of mass should be such that the total initial displaced volume $V(t=0)$ should be within $5\%$ of the total displaced volume at the end of the computation $V(t=T)$ where $T$ represents the computation end time. It is assumed that the end of the computation is when the initial wave is entirely reflected and offshore.