 |
 version |
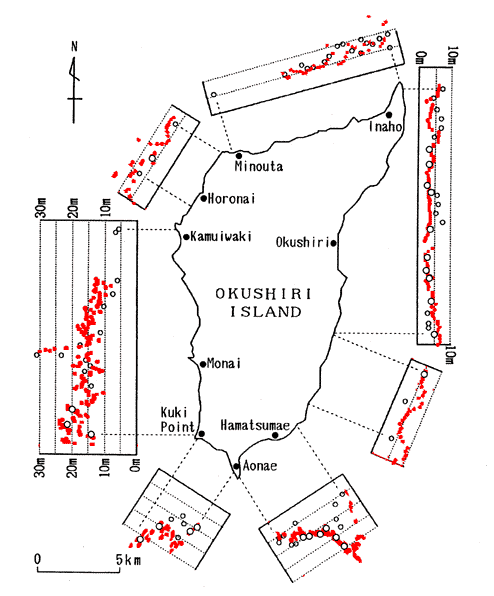
Figure 1. Comparison of field measurements (empty circles) with VTCS-3 inundation predictions (solid circles). |
Recent advances in hydrodynamics through validation of model results with large-scale laboratory experiments [Titov and Synolakis, 1993, Yeh et al., 1994 Liu et al., 1995, Briggs et al., 1995] have demonstrated excellent predictive capabilities of the state-of-the-art inundation algorithms, yet the extrapolation of these results to prototype tsunamis is not unequivocal. In the physical models, idealized and well-defined solitary waves evolve over constant depth and then over idealized bathymetry, while in nature the initial wave profile is never known in detail, and the wave propagates over complex bathymetry and climbs up topography known only to finite resolution ; the latter was not believed to be an important constraint, given that typical tsunami wave scales are larger than microtopographic features, until recent field data demonstrated otherwise [Yeh et al., 1993; Synolakis et al. 1995].
The Mw = 7.8 Hokkaido-Nansei-Oki earthquake of July 12, 1993 was a fortuitous large-scale experiment which allowed the measurement of high-quality runup data and the inference of fairly unambiguous ground deformation contours due to its proximity to seismic instrument arrays in a locale where high-resolution bathymetry and topography data exist. Hydrodynamic computations reported to date [Myers and Baptista, 1995, Satake and Tanioka, 1995, Takahashi et al., 1995] using the shallow-water wave approximation (SW) have reproduced to first-order the runup heights distribution along the coast of Hokkaido and to some extent around Okushiri, but neither the wave current velocities nor the extreme runup values observed in the front of the island; at best [ Takahashi et al., 1995], predictions for the extreme measurements have differed by a factor of two from the field data. Further, the region of most extensive devastation did not correlate well with the highest measured runup. Given that the Hokkaido-Nansei-Oki event was not a tsunami earthquake [F. Schindelé et al, 1995], i.e., an earthquake which produces a tsunami disproportionally large for its size, these differences are intriguing, and they have implications in planning for large tsunami disasters.
To explore the relative effects and magnitudes of of inundation heights and inundation-flow velocities, and to determine whether the modeling difficulties are due to inherent limitations of the SW models or their application outside their range of validity or to splash, or to resolution limits, or even whether to the notoriously difficult [Aida, 1977, Iwasaki and Mano, 1979, Hibberd and Peregrine, 1979, Shuto, 1991, Liu et al., 1991] and unstable [Synolakis, 1989] shoreline computations, we investigated this tsunami using a new inundation model.
| ht + (uh)x + (vh)y | = 0, | |
| ut+ uux + vuy + ghx | = gdx, | (1) |
| vt+uvx + vvy + ghy | = gdy. |
Here h = h(x,y,t) + d(x,y,t), where h(x,y,t) is the amplitude, and z = -d(x,y,t) is the location of the bottom with respect to the undisturbed water surface, while u(x,y,t), v(x,y,t) are the depth-averaged velocities in the onshore x and the longshore y directions respectively; g is the acceleration of gravity. These equations are believed to model the dynamics of the runup process well. To avoid confusion, we will refer to these equations as the 2+1 NSW equations to indicate that there are two spatial propagation dimensions and one temporal one; the 1+1 NSW equations only model wave evolution in the x direction. We solve without adding dissipation terms. Although physically bottom friction does affect the wave evolution, it has been shown [Kobayashi et al., 1987, Zelt, 1991, Kobayashi, and Wurjanto, 1992, Liu et al., 1995, Raubenheimer and Guza, 1996] that inundation results are not sensitive to changes in the roughness coefficient, at least when these results are compared with laboratory data. Also, since the bottom-friction coefficient can only be inferred from related studies or by model self-calibration, we do not use it, particularly because we have found our method sufficiently robust.
We will use explicit finite-differencing and we will split the system of three 2+1 coupled equations (1) into two 1+1 quasi-linear systems. Note, that the conventional practice is to use an implicit scheme with the splitting method for solving the resulting one-dimensional equations; this approach works well for elliptic and parabolic equations, reducing the number of operations substantially compared with applying an implicit scheme applied directly on the 2+1 equations [Fletcher, 1991]. Here, (1) is a hyperbolic quasi-linear system, yet we did find it advantageous to use the splitting method in combination with an explicit FD technique. The main advantage is the use of the characteristic form of the 1+1 NSW equations, which allows the definition of of a well-posed boundary value problem for the numerical method. The characteristic form of equations also allows for an efficient FD realization [Titov and Synolakis, 1995], using the fractional step method of Yanenko [1971].
The most critical step in the inundation calculation is the shoreline computation, which involves a moving boundary interface between three different phases, liquid air and solid. The 1+1 shoreline computation was a classic problem of hydrodynamics and it is discussed in detail by Shuto [1991]. 2+1 inundation calculations have been reported recently [Shuto, 1991, Myers and Baptista, 1995, Takahashi et al., 1995 , Liu et al., 1995], but all include friction factors.
In our inundation computations, it is impossible to use the direct relationships between the Riemann invariants near the shoreline, since here the Froude number may be greater than one, and all characteristic families have the same inclination in this region. Therefore, we use approximations of the boundary values from previous space nodes. Our shoreline algorithm uses the time-dependent space step Dx(t) of the last node of the computational area. The objective is maintain the shoreline boundary point on the surface of the beach during the computation, as first suggested by Iwasaki and Mano [1979]. By adjusting the length of the last space-step every time-step, we ensure so that the shoreline point is at the intersection of the beach with the horizontal projection of the last "wet" point. The value of the velocity on the shoreline node is equal to the velocity of the previous "wet" point. We will refer to our method henceforth as VTCS-3; it has been shown in excellent agreement with data from large-scale laboratory experiments on wave runup on circular islands [Titov and Synolakis, 1995], even for mildly plunging waves, where the energy dissipation of the physical manifestation is modeled through our particular FD scheme's inherent dissipation.
Since our objective is to primarily evaluate the predictive power of the hydrodynamic model under extreme conditions and not the relative merits of different source models, we will only use the three-fault plane dipole-shaped ground deformation model of Takahashi et al. [1995], known as DCRC-17a, as our initial condition. DCRC-17 predicts a maximum uplift of 4.2m and subsidence of 1.1m, and hydrodynamic calculations using it have produced the closest qualitative agreement with the field observations to date among different source models [Myers and Baptista, 1995, Takahashi et al., 1995, Myers and Baptista, 1995, Satake and Tanioka, 1995].
Finally, in our simulations we used the digitized bathymetry as provided by the Disaster Control Research Center in Tohoku University consisting of several nested bathymetric arrays with three level of grid resolution, ranging from 450m offshore to 50m in several locations close to the initial shoreline.
 |
 version |
Figure 1. Comparison of field measurements (empty circles) with VTCS-3 inundation predictions (solid circles). |
The extreme 31.7m measurement near Monai was computed as 29.7m. The measurement was made at the tip of a small canyon and it is undoubtedly a local effect; yet all measurements around it were consistently high with a global maximum at 31.7m, similar to the distribution of computed values shown in the figure; this measurement distribution was not present in the other simulations [Myers and Baptista, 1995, Satake and Tanioka, 1995]. Takahashi et al [1995] produced qualitatively and quantitatively correct distributions, but only predicted maximum runup of 15m in this locale; we speculate that their friction factor disproportionally affect the larger values. Most of our computed runup values are a slightly higher than measured, but then our model does not include any dissipation. The largest difference is near Inaho at the north, where the calculations predict 15m heights compared to the 10m field measurements [Hokkaido Tsunami Survey Group, 1993] ; interestingly, 12-15m field mearurements have been reported at Inaho by other japanese reconnaissance teams [Nakasuji and Takahashi, 1993]. Overall, for this extreme tsunami event the SW model appears adequate for modeling runup heights, suggesting that wave breaking and bottom friction are apparently not important to first-order for predicting inundation.
 |
 version |
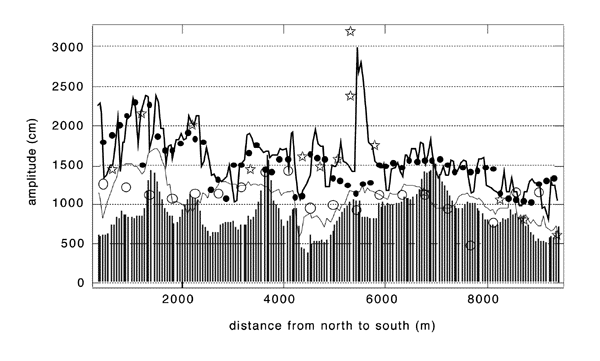
Figure 2. Comparison of obsrvations (stars) with inundation model using different grid resolutions and depth-threshold model predictions. |
We then performed a series of numerical experiments to evaluate the effect of other aspects of numerical modeling, such as the grid resolution and the 10m-depth threshold. Figure 2 compares runup results among computations with different grid resolutions for a region of the west coast of Okushiri island where topographic data exist down to 50m-square resolution. For reference, the leading N-wave close to the shoreline [Tadepalli and Synolakis, 1995&1996] has a O (1km) wavelength , and therefore the computations shown range from 3-4 points per wavelength for the 450m grid to 20 points per wavelength for the 50m grid. This number may appear small by computational fluid dynamics standards (CFD) standards, but then as Shuto [1991] pointed out, the effects of the grid resolution are often counterintuitive, because of numerical dispersion.
The computations with the 150m grid produce qualitatively correct runup distribution, but miss the extreme runup height. The computations with the 450m grid, even though adequate in terms of hydrodynamic stability to resolve the waveform [ Titov and Synolakis, 1995], these calculations seriously underpredict the runup height, suggesting that it is the effect of the small-scale features hidden in the coarse grid and not only the effect of wavelength resolution. This is rather important, as problems arising only from wavelength resolution can be solved easily by generating denser grids (through interpolation of the coarser grid), yet these denser grids have identical topography resolutions as the coarse grids that produced them.
In figure 2, we also present results from numerical experiments we did to compare the predictions of models with 10m-contour calculation thresholds. These models are still ubiquitous [Yeh et al., 1993, Synolakis, et al. 1995, Satake and Tanioka, 1995]; and they propagate the wave using a NSW model up to the 10m contour, and then use the maximum wave height at that location to infer the maximum runup height. For identical grid resolutions, our results show that interrupting the computation at the 10m depth, a step essentially equivalent to placing reflective "wall"-type boundaries at that depth, underpredicts the runup by a factor of two, as compared with the inundation computations. Even the computed maxima at the 10m contour from the full inundation calculation differ substantially from the computed maxima from the 10m-threshold "wall" calculations, suggesting that the practice of using the waveheight at the 10m depth to infer the runup to first order needs to be re-evaluated. Clearly the wave evolves substantially as it propagates from the 10m depth up the beach to its maximum runup.
 |
 version |
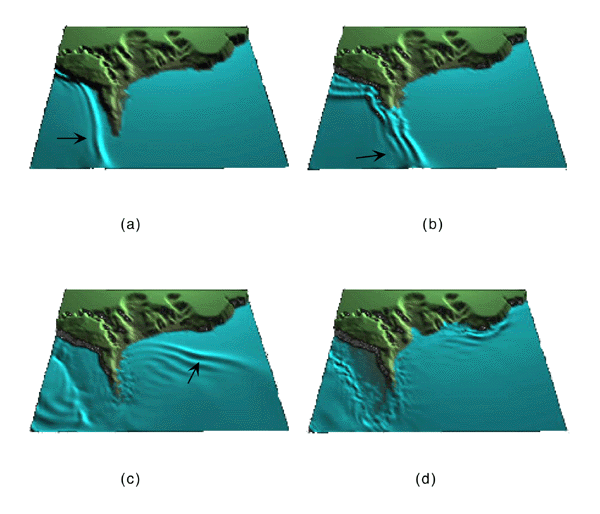
Figure 3. Snapshots of the computed overland flow in Aonae, at 5 min (a), 6 min (b), 8 min (c) and 12 min (d) after the earthquake. |
Another challenging computation for the SW theory is overland flow, a condition referring to waves overtopping a peninsula or a narrow strip of land sandwiched between the ocean and a tidal inlet, then propagating over it and then draining on the lee side of the land. Overland flow was first described by Yeh et al. [1993], and later identified [Synolakis et al., 1995] as one of the leading causes of the heavy casualties during tsunami attack because of the high flow velocities; during tsunami runup on a sloping beach, the shoreline fronts slows down as its kinetic energy is converted into potential energy, but during overland flow over flat land the kinetic energy is only reduced by dissipation. Overland flow is usually supercritical with bore-like dynamics. We present overland flow results near Aonae in the four flow snapshots of figure 3, before, during and after the overland flow. The dynamics are very similar to those inferred from the field observations [ Hokkaido Tsunami Survey Group, 1993, Shimamato, 1995]. The computed flow velocities range from 10-19 m/s over the Aonae peninsula, consistent with the 10-18 m/sec field estimates of in Aonae [Shimamato, 1995]. These values are consistently higher compared with elsewhere around the cape and they correlate well with the devastated area.
 |
 version |
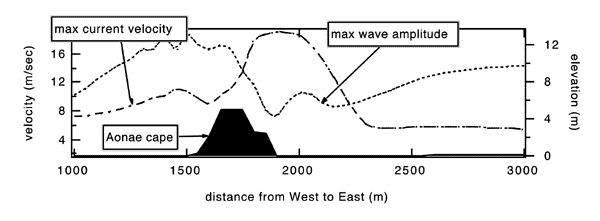
Figure 4. Computed envelope of maximum tsunami heights and of maximum wave velocities over one typical topographical cross-secsion of Aonae cape. |
Figure 4 presents the envelope of maximum tsunami heights and of maximum wave velocities over one typical topographic cross-section of Aonae cape.
Notice that the highest inundation velocities occur at the east side of Aonae where inundation heights are smallest, and how these extreme velocities correlate at least qualitatively with the most devastated area. This is entirely consistent with the fact that the during the lee-side rundown of the overland flow, the flow depths are small, but the flow is supercritical with large flow velocities, and it underlines the risk of relying exclusively on runup heights to predict inundation.
Despite the inherent difficulties of comparing tsunami field data with model predictions, we conclude that the SW approximation and current state-of-the-art solution methods are capable of modeling quantitatively correctly the tsunami inundation, including extreme runup heights and inundation velocities. We find that even small local bathymetric structures affect the runup to first-order and that the resolution of the bathymetric data maybe more important than the grid resolution. Our results also suggest-albeit only qualitatively- that during overland flow, coastal devastation correlates stronger with inundation velocities than inundation heights. This difference along with the often substantial wave evolution from the 10m depth to the maximum runup suggest caution in interpreting threshold-depth type calculations as they may miss extreme events.
Acknowledgements. We thank Mamoru Takahashi from Kokusai Kogyou Co. for providing the aerial photograph of the Aonae Cape and Dr. Tomu Takahashi of DCRC of Tohuku University for the digitized bathymetry. We are grateful to Dr. Cliff Astill of the Natural Hazard Mitigation Program of the National Science Foundation for supporting the development and validation of our research.