Edge Wave and Non-Trapped Modes of the 25 April 1992
Cape Mendocino Tsunami
F.I. González1, K. Satake2, E.F. Boss3, H.O. Mofjeld1
1Pacific Marine Environmental Laboratory/NOAA
7600 Sand Point Way, N.E.
Seattle, WA 98115, USA
2Dept. Geological Sciences
University of Michigan, 1000 CC Little Bldg
Ann Arbor, MI 48109, USA
3Joint Institute for Study of Atmosphere and Ocean
University of Washington
Seattle, WA 94195, USA
Abstract - The 25 April 1992 Cape Mendocino earthquake generated a tsunami characterized by both coastal trapped edge wave and non-trapped tsunami modes that propagated north and south along the U.S. West Coast.
Both observed and synthetic time series at Crescent City and North Spit are consistent with the zero-order edge wave mode solution for a semi-infinite sloping beach depth profile.
Wave amplitudes at Crescent City were about twice that observed at North Spit, in spite of the fact that the source region was three times farther from Crescent City than North Spit.
The largest observed amplitude was due to an edge wave which arrived almost 3 hours after the initial onset of the tsunami; since such waves are highly localized nearshore, this suggests that the enhanced responsiveness at Crescent City is at least partly due to local dynamic processes.
Furthermore, the substantially delayed arrival of this wave, which was generated at the southern end of the Cascadia Subduction Zone, has significant implications for hazard mitigation efforts along the entire U.S. West Coast.
Specifically, this study demonstrates that slow-moving but very energetic edge wave modes could be generated by future large tsunamigenic earthquakes in the CSZ, and that these might arrive unexpectedly at coastal communities several hours after the initial tsunami waves have subsided.
Key Words:
Tsunami, Edge Waves, Cape Mendocino, Cascadia Subduction Zone, Hazard Mitigation.
Introduction
On 25 April 1992, a tsunami was generated by a magnitude 7.1 earthquake at the southern end of the Cascadia Subduction Zone (CSZ), near Cape Mendocino, California (Oppenheimer, et al., 1993).
The waves propagated north and south along the California and Oregon coast and were recorded at nine tide gage stations maintained by the National Oceanic and Atmospheric Administration (NOAA).
The measurements are presented in Figure 1.
Although the waves in this event were small and not destructive, they have both intrinsic scientific interest and important implications for hazard assessment and mitigation along the California, Oregon and Washington coast.
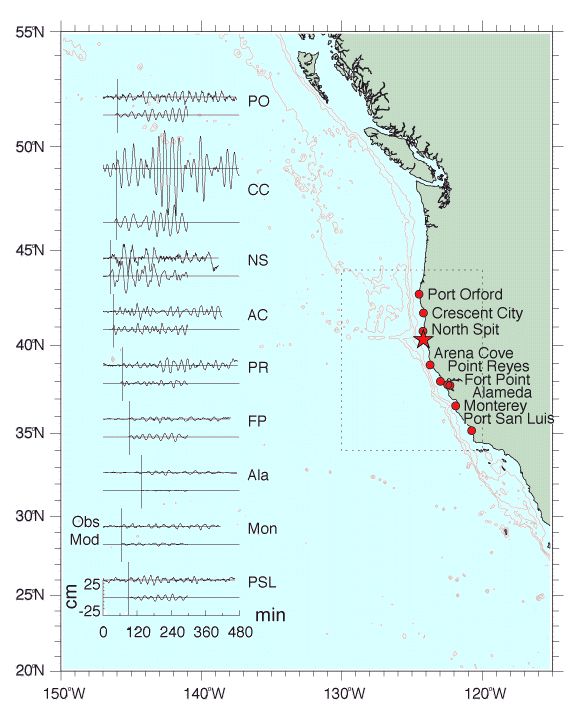
Figure 1
Summary chart presenting observed (top) and computed (bottom) time series for nine tide gage stations along the coasts of California and Oregon.
Vertical axes are deviation from background sea level in cm; horizontal axes are minutes of elapsed time after the main shock, with a vertical line indicating the computed arrival time at each station listed in Table 1.
Bathymetric contour interval is one kilometer.
The dotted line rectangle denotes the numerical model computational region.
Cape Mendocino is just south of North Spit, and the solid star marks the earthquake epicenter.
The practical implications of this event are related to the potential hazard posed by future large tsunamigenic earthquakes along the U.S. West Coast.
Although the Cape Mendocino earthquake was large and inflicted substantial damage on land, the shallow dip angle of about 12 degrees induced vertical motion of the offshore ocean bottom of less than 1 m, producing correspondingly small ocean waves.
However, there is increasing geological and seismological evidence that great (M > 8) earthquakes have previously occurred in the CSZ, and that these earthquakes have generated much larger, destructive tsunamis (Atwater, 1987; Heaton and Hartzell, 1987; Weaver and Shedlock, 1992) .
Furthermore, recent events in Japan (Bernard, et al., 1993), Indonesia (Yeh, et al., 1993), and Nicaragua (Kanamori and Kikuchi, 1993; Satake, et al., 1993) have demonstrated that earthquakes as small as magnitude 7.1 can generate tsunamis capable of devastating communities in the near-field, i.e., within a wavelength or so of the generation region (also see other articles in this issue on these tsunamis).
Finally, the edge waves which accompanied the Cape Mendocino tsunami add a new dimension to the hazard along this coastline by virtue of two defining characteristics.
First, such waves are coastal trapped, i.e. their amplitude is a maximum at the coastline and rapidly decays seaward; second, they propagate slowly along the coast and thus, depending on source distance and geometry, can arrive at coastal communities hours after the highest non-trapped tsunami wave incident from deeper water offshore.
Near-source communities on the U.S. West Coast may thus be confronted by a hazard that has both a rapid onset and long duration; i.e., the non-trapped tsunami may strike from offshore in the first few minutes, then be followed hours later by slow-moving but energetic edge waves trapped along the coast.
Scientifically, edge wave research has a long and venerable history (Stokes, 1846; Eckart, 1951; Ursell, 1952; Ball, 1967), and their presence makes this event particularly interesting.
They are apparently ubiquitous along the California coastline as a low level continuum of background noise; but more energetic modes can be excited by a number of mechanisms, including interactions with swell energy, atmospheric disturbances, and tsunamis incident on the coast from deep water (Greenspan, 1956; Munk, et al., 1956; Fuller and Mysak, 1977).
The present case is especially interesting because the tsunami edge waves were directly generated in the nearshore region by impulsive vertical motion of the ocean bottom; they then propagated north and south from Cape Mendocino, trapped nearshore within the coastal wave guide for edge waves.
The purpose of this study is to present a simple but plausible analysis of the coastal tide gage time series that establishes the presence of both non-trapped and coastal trapped modes of tsunami wave energy.
We will do this by comparing and interpreting the observations with both numerical model simulations and simple edge wave theory.
Although both modes are tsunami waves, in conformance with common usage and for ease of exposition in what follows we will sometimes refer to the non-trapped tsunami mode simply as the "tsunami," and to the coastal trapped tsunami modes as "edge waves."
Generation Mechanism: Impulsive, Nearshore Ocean Bottom Displacement
Figure 2 presents model results for the static vertical displacement of land and ocean bottom induced by crustal motion on a simple, rectangular fault plane (Okada, 1985).
We used values for the fault plane parameters of 21.5 km length, 16 km width, 6.3 km depth, 342° strike, 12° dip, 107° rake, 2.7 m slip, with a rigidity value of 3 x 1011 dyn/cm2, with the plane situated such that the epicenter at (40° 18.08' N, 124° 11.80' W) was located in the southeast corner.
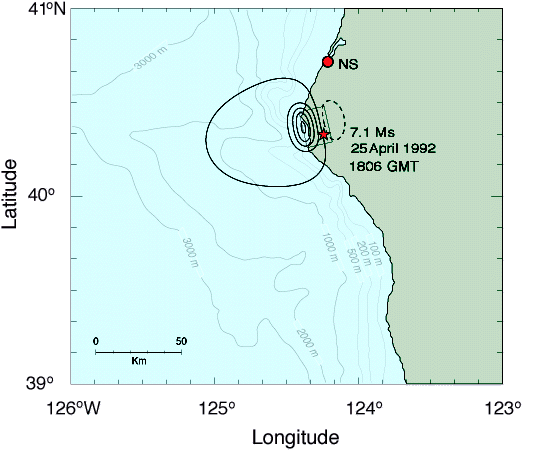
Figure 2
Computed vertical crustal deformation for a single fault plane model.
Heavy, solid contours represent uplift, dashed subsidence; the first solid contour is 0.2 cm, and all other contours are at 20 cm intervals.
The solid line rectangle delineates the surface projection of the fault plane (see Generation Mechanism section in text for fault plane parameters), and the location of the epicenter is indicated by a star.
This is the optimal fault plane model as described by Oppenheimeret al. (1993), and represents the best fit of vertical and horizontal model displacements to all available observations acquired from GPS and Geodolite measurements inland of the coast, and from organism die-off horizons induced by uplift along the coast.
A very reasonable fit to field observations is thereby obtained, although model variations are smoother and individual field measurements are somewhat higher.
Good qualitative agreement is thus expected between reality and the model, although the real distribution of vertical displacement is probably not as smooth as the dipole pattern produced by this idealized model.
As can be seen, the nearshore uplifted region delineated by the 20-cm level contour can be characterized as an ellipsoid with major and minor axes approximately 30 and 25 km long, respectively, with the major axis oriented in the local alongshore direction, and with the center located about 5 km offshore.
The duration of this displacement was on the order of 10 s (Y.tanioka, et al., 1994), i.e., short enough to be considered an impulsive ocean wave generation mechanism (Hammack, 1973).
Coastal Sea Level Measurements
Analog tide gage records from each station were provided by NOAA's National Ocean Service.
Unfortunately, only digital data with a 6-min sampling period was available for Arena Cove.
The analog records were digitized at a sampling rate of 15 s, then subjected to a 2-90 min band-pass filter to remove the tides.
To aid in the identification of tsunami energy in the tide gage records, we also performed travel time computations for selected West Coast stations using an iterative grid refinement technique (Braddock, 1969).
The computations assume that the deep water tsunami waves travel at the long wave group velocity, (gh)1/2, where g is the acceleration due to gravity and h the water depth.
The results are summarized in Table 1, and are also presented graphically in Figure 1 in the form of vertical lines that intersect the time axes of the individual time series plots.
Table 1
Wave ray travel time computations, assuming propagation speed cg=(gh)1/2
| Station |
Travel Time
(min) |
|---|
|
| Port Orford |
50 |
| Crescent City |
47 |
| North Spit |
26 |
| Arena Cove |
37 |
| Point Reyes |
69 |
| Fort Point |
94 |
| Alameda |
135 |
| Monterey |
64 |
| Port San Luis |
97 |
At the tide gage station nearest the epicenter, North Spit (in Humboldt Bay), a very small positive wave is observed to arrive after about 25 min.
Here, the clear positive sense of the first wave is consistent with the uplift assumed in the generating region (Figure 1).
Two distinct wave packets are evident, with the second arriving about 135 min after the main shock.
The first wave packet is more energetic than the second, with maximum positive amplitudes of 20 and 15 cm, respectively, and the arrival time of the first is consistent with the computed estimate of 26 min (Table 1, Figure 1), corresponding to a wave ray path (not shown) that traverses deeper offshore water.
However, the largest amplitudes (about twice that at North Spit) were recorded at Crescent City, even though this station is three times more distant from the source region than North Spit (Figure 1).
Again, two well-defined packets of wave energy are apparent in the first five hours of the record.
In contrast to North Spit, however, the second packet is more energetic than the first with maximum positive amplitudes of 53 and 35 cm, respectively.
Neither the precise arrival time nor the polarity (positive or negative sense) of the first wave are clear in this record, due to the presence of background noise.
However, the arrival of the first packet of tsunami wave energy is again consistent with the travel time estimate of 47 min (Table 1, Figure 1), corresponding to the non-trapped mode.
The second wave packet arrives about 155 min after the main shock; the analysis presented below suggests that these are coastal trapped waves, i.e. edge waves, characterized by much slower propagation speeds and by amplitudes which decrease rapidly with distance offshore.
As previously noted, the Arena Cove record suffers from a longer sea level sampling interval (6 min) than that of the other stations (15 s), so that waveforms may be somewhat distorted.
Nonetheless, it is again apparent that two packets of tsunami energy are present, the first arriving about 35 min and the second about 210 min after the main shock.
At Point Reyes, a very small amplitude, low frequency wave packet arrives after 65 min, followed by a larger amplitude packet which arrives 180 min after the main shock.
Much weaker signals are discernible at Fort Point and Alameda in San Francisco Bay, starting at about 90 and 110 min, respectively; it is possible to identify and match individual features in these two records, as the wave propagates into the bay with relatively little distortion.
At Monterey, a weak low frequency signal is also seen to arrive at about the predicted time of 64 min.
Taken together, the last four stations demonstrate the importance of two local bathymetric features -- Monterey Canyon, just offshore of Monterey Bay, and the broad shelf region that extends north from the canyon to Arena Cove.
Thus, the tsunami arrives at Point Reyes and Monterey at about the same time, even though Monterey is 200 km farther south; this is because the speed of the tsunami is significantly reduced in the relatively shallow approach to Point Reyes, but increased in the deeper waters offshore of Monterey.
The significantly later arrival times at Fort Point and Alameda, inside San Francisco Bay, also reflect the influence of the broad, shallow shelf outside the bay, the relatively narrow entrance to the bay, and the shallow depth of the bay itself.
Both the extreme southern and northern West Coast records, Port San Luis and Port Orford (Figure 1), are difficult to interpret.
The first two hours of each are somewhat noisy, but coherent low frequency oscillations appear to begin at about the predicted arrival times.
It is unclear whether more than one wave packet is present in either record.
At Point Arguello and Point Concepcion, just south of Port San Luis, there is an abrupt change in the trend of the coastline (Figure 1).
Evidently, no significant wave energy propagated around and to the southeast of this feature, since records we examined for stations along this coast displayed no tsunami signal.
Numerical Model Results
Tsunami propagation was simulated as an initial value problem, by integrating the nonlinear long wave equations with friction by means of a leap-frog finite difference scheme with upwind advection terms (Satake, 1994).
Boundary conditions required zero normal flow at the coastline, and a constant sea surface slope was maintained at open ocean boundaries through application of a radiation condition (Hwang, et al., 1972).
The integration time step was 5 s, the resolution of the computational grid was 1 arc-minute, and the computational region extended over the 10 degree by 10 degree rectangle delineated by the dotted line in Figure 1.
Initial sea level values were specified by assuming that the ocean surface instantaneously conformed to the ocean bottom displacement while horizontal water velocities were set to zero.
We note that, as a consequence of the position and orientation of the modeled crustal displacement (Figure 2), the initial sea surface displacement was characterized as a mound of water with a maximum value of 80 cm situated less than 5 km offshore in 50-100 m of water, an alongshore length scale of about 30 km, and an offshore length scale of about 8-10 km extending from the coast to about the 500 m bathymetry line.
The observed and computed records at the eight coastal tide gage stations are compared in Figure 1.
The agreement in period and phase of individual waves is quite good at all stations and, although amplitudes do not agree as well, individual wave packets with 2-5 cycles per group are reproduced at several stations.
First wave arrivals of both model and observations at each station agree well with those predicted by wave ray tracing (Table 1, Figure 1).
These initial waves are thus the non-trapped tsunami waves traveling with group velocity (gh)1/2 and have minimized their travel time by propagating along paths traversing the deeper offshore water associated with higher group speeds.
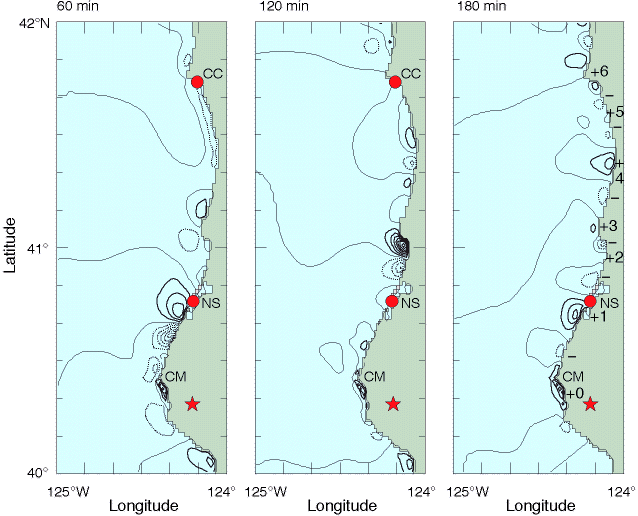
Figure 3
Sea level distributions computed by the tsunami numerical model at 60, 120, and 180 min after generation; contour interval is 5 cm, and solid and dotted lines indicate values above and below mean sea level, respectively.
At 180 min, six cycles of edge wave extrema along the coast are marked by numbered plus signs and unlabeled minus signs.
(The extrema are actually at the coastal boundary, not offshore; see text for explanation.)
The star marks the position of the earthquake epicenter, and the locations of Cape Mendocino (CM), North Spit (NS) and Crescent City (CC) are also indicated.
In the next section, we show that the subsequent wave packets are edge waves, i.e. waves characterized by rapidly decreasing amplitude offshore (trapped), and very slow speeds of alongshore propagation.
This is clearly seen in Figure 3, a series of snapshots of computed sea level, in which individual, coastal trapped waves can be seen propagating alongshore away from the source region.
(Note that in these figures, maximum and minimum values are actually at the coast, not offshore; the apparent offshore locations of these extrema are false artifacts of the contouring algorithm, which interpolates and inserts contour lines between zero-value land cells and adjacent non-zero sea level values.)
Edge Wave Analysis
The simplest bathymetry that gives rise to edge waves is a one-dimensional semi-infinite sloping beach for which depth, h, increases linearly with the offshore coordinate, x, as
where s is a constant and represents the slope of the beach.
In this case, solutions exist which decay exponentially offshore and are sinusoidal in the alongshore coordinate, y.
They are of the form (e.g. LeBlond, 1978; Mei, 1983)
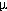 n(x,y) = A ei(kny-wnt) e-knxLn(x). n(x,y) = A ei(kny-wnt) e-knxLn(x). | | | | (2) |
Here, n is the mode number, 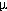 n is the wave amplitude, kn is the alongshore wave number, wn is the angular frequency, and the Ln(x) are the n-th order Laguerre polynomials, of which the first three are
n is the wave amplitude, kn is the alongshore wave number, wn is the angular frequency, and the Ln(x) are the n-th order Laguerre polynomials, of which the first three are
| L0(x) = 1 |
| L1(x) = (1-2k1x) | | | | (3) |
| L2(x) = (1-4k2x + 2k22x2). |
The dispersion relation for each mode is then given by
The phase and group velocities can then be written, respectively, as
| c = wn/k = [(2n+1) sg/k]1/2 | | | | (5) |
| cg = dwn/dk = 1/2 [(2n+1) sg/k]1/2 = c / 2 | | | | (6) |
where the mode number subscript on the variables c, cg and k are not explicit, but understood in context.
We note that these phase speeds are equivalent to that of a deep water gravity wave multiplied by the beach slope and a factor dependent on the mode number.
The phase speed thus increases with mode number, but low modes on beaches of small slope propagate much more slowly than either deep water gravity waves at the same frequency or long, shallow water gravity waves such as tsunamis.
These edge waves are also highly dispersive with the group speed only half that of the phase speed.
If these dispersive edge waves were impulsively generated as a mound of water similar to the displacement pattern shown in Figure 2, then the initial mound should evolve into a wave group traveling at celerity cg, with individual wave crests propagating through the group at the higher phase speed, c.
In particular, we expect the maximum of the mound to travel at the group velocity, so that arrival of the group maximum can be used to estimate the group velocity as
cg =  r/ r/ t t | | | | (7) |
where  r is the distance traveled and
r is the distance traveled and  t is the elapsed time from generation.
t is the elapsed time from generation.
Figure 4
Observed and modeled time series (top of each panel) and temporal evolution of the amplitude spectra (bottom of each panel) for Crescent City and North Spit.
In the spectral plots, note that the contour interval of the Crescent City observations [4(a)] is 5 cm, while contour intervals of the other three spectra are 1 cm; shading has been added to facilitate differentiation of local maxima (relative brightness) and local minima (relative darkness).
The nearshore bathymetry to the north of Cape Mendocino is simpler and more reasonably modeled as a semi-infinite beach (Eq. 1) than that to the south.
However, the quality of our numerical model bathymetric grid also degrades somewhat north of Crescent City; this is because high quality, 15 arc-second resolution NOAA bathymetry was not available north of 42°.
Luckily, the wave amplitudes are highest and the signal to noise ratio are most favorable at North Spit and Crescent City, stations that are located nearest the generation region and in the area of our most reliable bathymetric data (Figure 1).
For these reasons, we focus our analyses on these two stations.
The bathymetric data provide estimates of  r, the propagation distance along the coast from the generation zone to the observation point, and estimates of the mean bottom slope near the coast, s.
We computed
r, the propagation distance along the coast from the generation zone to the observation point, and estimates of the mean bottom slope near the coast, s.
We computed  r as the distance along the 50 m depth contour from the generation region to Crescent City and North Spit, and found them to be 59 km and 174 km, respectively.
We next computed the mean depth profile for the offshore region extending from the generation area to Crescent City; successive linear least square fits to the first 10, 20, and 25 km of this profile yielded estimates of s = .008, .010 and .011, respectively, so that s
r as the distance along the 50 m depth contour from the generation region to Crescent City and North Spit, and found them to be 59 km and 174 km, respectively.
We next computed the mean depth profile for the offshore region extending from the generation area to Crescent City; successive linear least square fits to the first 10, 20, and 25 km of this profile yielded estimates of s = .008, .010 and .011, respectively, so that s  .01 appears to be a robust estimate over the first 25 km.
.01 appears to be a robust estimate over the first 25 km.
The tide gage observations provide estimates of  and
and  t.
To aid in the estimates of these two parameters, both observed and computed time series at North Spit and Crescent City were subjected to an analysis of the temporal evolution of their energy spectrum (Dziewonski, 1969); the results are presented in Figure 4.
Table 2 summarizes these estimates, and Table 3 provides a comparison of observed group velocities with the first three theoretical edge wave modes.
t.
To aid in the estimates of these two parameters, both observed and computed time series at North Spit and Crescent City were subjected to an analysis of the temporal evolution of their energy spectrum (Dziewonski, 1969); the results are presented in Figure 4.
Table 2 summarizes these estimates, and Table 3 provides a comparison of observed group velocities with the first three theoretical edge wave modes.
Table 2
Estimates of wave group parameters at Crescent City and North Spit (refer to Figure 4)
| Station | Wave Group |
f= /2 /2
(cpm) |
T=1/f
(min) |
 t t
(min) |
 r r
(km)
|
cg
(km/min) |
|---|
| Crescent City |
Second Observed |
.0412 |
24.3 |
234 |
174 |
0.74 |
| Crescent City |
Second Modeled |
.0407 |
24.5 |
230 |
174 |
0.75 |
| North Spit |
First Observed |
.0348 |
28.7 |
89 |
59 |
0.66 |
| North Spit |
First Modeled |
.0326 |
30.7 |
77 |
59 |
0.76 |
Table 3
Comparison of edge wave theory and observations
| Station |
n |
k
(km-1) |
L=2  /k /k
(km) |
Computed cg
(km/min) |
Observed cg
(km/min) |
|---|
| Crescent City |
0 |
0.1895 |
33.2 |
0.68 |
0.74 |
| Crescent City |
1 |
0.0632 |
99.5 |
2.05 |
0.74 |
| Crescent City |
2 |
0.0379 |
165.8 |
3.41 |
0.74 |
| North Spit |
0 |
0.1358 |
46.3 |
0.81 |
0.66 |
| North Spit |
1 |
0.0453 |
138.8 |
2.42 |
0.66 |
| North Spit |
2 |
0.0271 |
231.3 |
4.03 |
0.66 |
At Crescent City, it appears that the n= 0 edge wave mode explains the observed group velocity of the second wave packet (Table 3).
Figure 5 graphically summarizes this simple model, presenting the mean profile data, the linear least square fit to these data, and the offshore (exponential) dependence of the zero-mode edge wave solution with unit amplitude at the coast, i.e., for Equations (2) and (3) with n= 0 and A= 1.
As a consistency check on the offshore length scales involved, we note that for n= 0 and k = 0.1895 km-1 (Table 3), the amplitude is reduced to 10% of the maximum value at an offshore distance of 12.2 km, comfortably within the 20-25 km offshore limit we have assumed for our simple model.
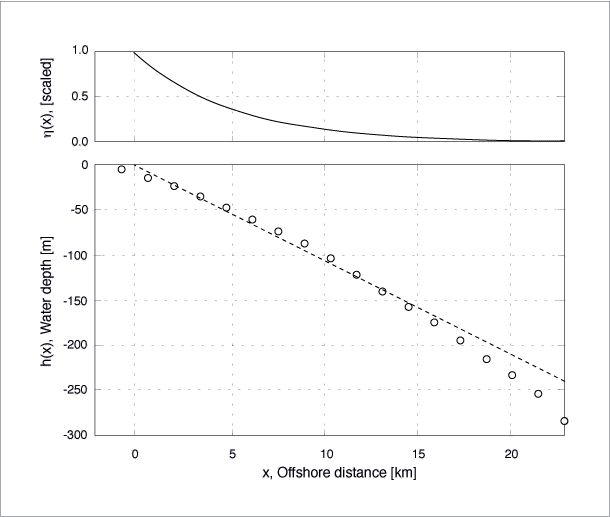
Figure 5
Lower panel presents the mean depth profile of the coastal region from Cape Mendocino to Crescent City (open circles), and the linear least square fit for the first 20 km offshore (dashed line).
The offshore distance indicated by the horizontal axis corresponds to the linear least square fit model.
The upper panel presents the offshore profile (scaled to unit amplitude at the coastline) of the zero-mode edge wave solution.
This agreement of Crescent City observations with simple edge wave theory allows us to recognize and interpret certain features of the numerical model results in terms of the underlying edge wave dynamics.
In the sea level distribution computed by the model at 180 min (Figure 3), six wave cycles are discernible over the distance of 174 km along the 50 m bathymetric contour from the generation region to Crescent City.
Although the separation between extrema varies due to bathymetric variations and coastline irregularities (Fuller and Mysak, 1977), the average wavelength of these six cycles is 29.0 km, which compares well with the zero-mode edge wave result of the simple theoretical model, L = 2 /k = 33.2 km (Table 3).
We thus believe that this feature of the numerical model reflects the dynamics approximated by the simple analytic theory for edge waves presented above.
/k = 33.2 km (Table 3).
We thus believe that this feature of the numerical model reflects the dynamics approximated by the simple analytic theory for edge waves presented above.
At North Spit, however, the interpretation is less straightforward.
The measured waveform is delayed relative to theory with an apparent group velocity that is 19% smaller than predicted (Table 3).
This discrepancy is primarily due to two factors.
First, the theory applies to the open coast while the observations were made inside of Humboldt Bay, about 1.5 km from the interior end of the narrow entrance channel that is approximately 0.6 km wide and 2 km long.
Consequently, wave propagation through the channel and into the bay should result in arrival times at the gage that are delayed relative to arrival at the coast.
Second, both non-trapped and edge wave mode tsunami energy are present in the first wave group of the North Spit record.
The relative amplitude and phasing of these two modes creates constructive and destructive interference that, in general, results in a hybrid wave group with different arrival time for the group maximum.
At Crescent City, these effects are also present but much less important because this station is substantially farther from the source.
As a consequence, delays in arrival at the gage relative to the coast are a smaller fraction of the total travel time, and superposition of the non-trapped and edge wave modes is minimized because their respective arrivals are well separated in time.
The first factor, the effect of a narrow channel entrance on tsunami propagation, has been simulated for Humboldt Bay by Whitmore (1993), who utilized a fine-scale computational grid (12 x 12 arc-seconds) and found that the waveform near the North Spit station was both attenuated in amplitude and delayed relative to arrival at the open coast ( P. Whitmore, private communication).
In contrast, our numerical model utilizes a relatively coarser computational grid with individual cells which are about three times the approximate width of the entrance channel.
However, we did not vary the frictional coefficient or the channel depth to delay the wave and improve agreement; as a consequence, our numerical model waveforms lead the observed by a few minutes at both Crescent City and North Spit (Figures 1 and 4).
The second complicating factor in the North Spit record, superposition of the tsunami and edge waves, can be illustrated by examining the period and expected arrival times of these two modes.
For the tsunami, note that the estimated arrival time at North Spit is 26 min (Table 1) and that the period at Crescent City is about 30 min (Figure 4a); thus, since the period should be invariant, the second tsunami wave cycle would arrive at North Spit 26 + 30 = 56 min after generation.
For the edge wave, the best estimates of period and group velocity are again those observed at Crescent City (Table 2), from which we can estimate an arrival time at North Spit of  t =
t =  r/cg = 59 km/0.74 km/min = 80 min for the center of a zero-mode group with a dominant period of 24 min.
Thus, the cycle preceding the center of the group would arrive at 80 - 24 = 56 min, i.e., about the arrival time estimated for the second tsunami cycle.
Thus, we conclude that the first wave packet observed in the North Spit time series (Fig 4b) is at least partly composed of the sum of both the non-trapped and the zero-mode edge wave tsunami modes.
r/cg = 59 km/0.74 km/min = 80 min for the center of a zero-mode group with a dominant period of 24 min.
Thus, the cycle preceding the center of the group would arrive at 80 - 24 = 56 min, i.e., about the arrival time estimated for the second tsunami cycle.
Thus, we conclude that the first wave packet observed in the North Spit time series (Fig 4b) is at least partly composed of the sum of both the non-trapped and the zero-mode edge wave tsunami modes.
Finally, we note that the expected arrival time of the first mode (n=1) at North Spit is  t =
t =  r/cg = 59 km/2.05 km/min = 29 min, and that of the second mode (n=2) is
r/cg = 59 km/2.05 km/min = 29 min, and that of the second mode (n=2) is  t = 59 km/4.03 km/min = 15 min (Tables 2 and 3).
Since Figure (4b) displays no significant energy during the first 50 min of the record, we conclude that the first and second edge wave mode energy is absent or negligible in the North Spit record.
Because they must traverse North Spit to reach Crescent City, we also conclude that these modes are absent in the Crescent City record.
t = 59 km/4.03 km/min = 15 min (Tables 2 and 3).
Since Figure (4b) displays no significant energy during the first 50 min of the record, we conclude that the first and second edge wave mode energy is absent or negligible in the North Spit record.
Because they must traverse North Spit to reach Crescent City, we also conclude that these modes are absent in the Crescent City record.
Discussion
The edge wave model we have used to interpret the observations is the simplest possible, i.e., a semi-infinite sloping beach, even though the actual physical setting deviates significantly from this ideal.
For example, although the mean depth profile presented in Figure 5 is reasonably well fit by a linear function, some curvature in the data is apparent, so that a quadratic or exponential fit (not shown) provides a better representation.
Furthermore, some alongshore variations in slope do occur, and coastal irregularities are not accounted for.
Nonetheless, the correspondence of observations, numerical model, and this very simple edge wave theory are quite convincing.
We believe that the essential features of the observed time series can be explained by the presence of both deep water tsunami waves and shallow water edge waves trapped along the coast.
A more detailed comparison and discussion of the observed and modeled time series is provided by the spectral evolution analyses presented in Figure 4.
The North Spit records in Figures 4(b) and 4(d) display excellent agreement in the most important parameters.
The main energy lobes are similar in both the amplitude and in the details of its structure and evolution in the frequency-time plane; this close match in the frequency domain reflects the remarkably close correspondence of individual features in the original time series.
There is, however, an interesting difference in a detail of the main lobes.
Both have a high frequency ridge, but that of the observations is more pronounced and oriented more vertically than that of the model.
Inspection reveals a vee-shaped trough in the observed time series after about 90 min has elapsed, while the corresponding trough in the model time series is more sinusoidal; in contrast, the peak that follows is more vee-shaped in the model than in the observations.
Higher frequency Fourier components are required to resolve such peaks and troughs, so the difference in the two ridges may be due to the difference in the location and severity of these sharp, non-sinusoidal features in the time series.
A more important disagreement in the two North Spit records is most clearly revealed as a difference in the location of the secondary lobe, which appears earlier and at a lower frequency in the observations.
This difference appears to be due to late arrival of edge wave energy in the simulation; small differences in the phasing of the deep water tsunami and edge waves could have produced the differences apparent in both the wave form and the spectral evolution diagram.
At Crescent City, there is also qualitative agreement between observed and modeled evolution of the spectra displayed in Figures 4(a) and 4(c).
Two wave groups are apparent which arrive at about the same time, and in each time series the second is more energetic than the first.
But important differences are also apparent.
The most striking is the disparity in amplitude; both the non-trapped and edge wave tsunami mode are observed to be two to three times larger than the model results.
The source of this discrepancy is not presently understood, but a number of factors could be responsible, e.g., errors in bathymetry or initial conditions.
The simulated non-trapped tsunami is also somewhat lower frequency than observed, and the observed edge waves are characterized by sharp, vee-shaped troughs that create a high frequency ridge absent in the modeled results.
Why were the largest waves observed at Crescent City rather than North Spit (Figures 1 and 4), even though Crescent City is located three times farther from the source than the North Spit station (Table 2)?
This is an important and interesting issue.
It is possible that the lower amplitudes observed at North Spit are due to destructive interference of tsunami and edge wave energy.
But the Crescent City community has a well known history of especially severe tsunami damage, and a number of investigators have suggested possible mechanisms that may make this area especially responsive to incident long wave energy.
Various studies of individual tsunami events have cited source directionality (Wiegel, 1976; Hatori, 1993 ), focusing of wave energy by offshore bathymetry (Roberts and Chien, 1964), and resonant shelf oscillations (Wilson and Torum, 1968) to explain high tsunami amplitudes at this location.
Houston and Garcia (1978) performed finite difference simulations of the 1964 Alaskan tsunami.
Their model results indicate that the high amplitudes on the West Coast were generally due to source directionality but that the Crescent City area in particular was also characterized by quite localized resonant response, extending over length scales only 2 to 4 miles (4 to 7 km) alongshore.
Both the coastal tide gage observations and our numerical model results are consistent with a mechanism involving local effects since the coastal trapped edge wave amplitudes are larger than the deep water tsunami waves in both the computed and observed Crescent City record.
Both the Crescent City and North Spit observations are characterized by additional wave groups that appear after the edge wave.
They are more pronounced at Crescent City, where they occur at approximately the same frequency as the first and largest edge wave, and are regularly spaced at intervals of about 100 min (Figure 4a).
The nature and origin of these waves is not clear, but we speculate that these observed characteristics may indicate a mechanism involving reflection of the zero-mode edge waves.
Summary and Conclusions
A small tsunami was generated at the southern end of the Cascadia Subduction Zone on 25 April 1992 by a magnitude 7.1 earthquake near Cape Mendocino, California.
Wave energy propagated north and south along the West Coast, and was detected at NOAA coastal tide gage stations in California and Oregon.
The records were characterized by several distinct wave groups arriving over the course of 8-10 hours.
We have processed these data to remove the tidal signal and isolate the energy in the tsunami frequency band and have estimated the temporal evolution of the spectra for each time series.
We have compared these records with arrival times estimated by wave ray computations, nonlinear long wave numerical model simulations and, for the records at North Spit and Crescent City, simple edge wave theory based on a linear fit to the mean depth profile.
We obtained consistent results between observations, model results and theory, and our analyses lead us to conclude
(1) that both non-trapped and coastal trapped edge wave tsunami modes were generated, and
(2) that the edge wave mode was the gravest, or zero-, mode with alongshore wavelengths of about 30 km and a maximum amplitude at the coast which decayed exponentially offshore with a length scale of 5-10 km.
Furthermore, since this event occurred at the southern end of the Cascadia Subduction Zone, it is particularly significant to issues of tsunami hazard mitigation along the adjacent California, Washington and Oregon coastlines.
At Crescent City, the edge wave packet was characterized by 50% higher amplitude, and therefore twice the energy, of the non-trapped tsunami mode and arrived several hours after tsunami waves were incident from offshore.
Much more energetic edge wave generation by future large earthquakes in the CSZ must therefore be considered a distinctly hazardous possibility.
In such a scenario a community might be subjected to a damaging tsunami within minutes of an earthquake, assume from the subsidence of these waves that the danger had passed, then be struck unexpectedly a number of hours later by even larger waves which had propagated slowly along the coast as trapped edge wave tsunami modes.
We thus also conclude
(3) that energetic edge waves generated by future tsunamigenic earthquakes in the CSZ pose an additional and particularly insidious hazard to U.S. West Coast communities, since the edge wave energy may appear unexpectedly, hours after the non-trapped tsunami waves have arrived and dissipated and
(4) that local dynamic processes may make Crescent City particularly responsive, and therefore more vulnerable, to such coastal trapped long wave energy.
Acknowledgments
Coastal tide gage records were provided by NOAA's National Ocean Service.
This study is contribution No. 1592 of the Tsunami Research Project in the Ocean Environment Research Division of NOAA's Pacific Marine Environmental Laboratory, and contribution No. 299 of the Joint Institute for the Study of the Atmosphere and Ocean.
Partial funding for this work was provided by NOAA's Coastal Ocean Program.
References
Atwater, B. F. (1987), Evidence for Great Holocene Earthquakes Along the Outer Coast of Washington State, Science, 236, 942-944.
Ball, F. K. (1967), Edge waves in an ocean of finite depth, Deep-Sea Res., 14, 79-88.
Bernard, E. N., González, F. I., Sigrist, D., Tsuruya, H., Kato, K., Shuto, N., Matsutomi, H., Tsuji, Y., Ito, H., Yamamoto, K., Iwasaki, Y., Sasaki, K., Hattori, A., Suzuki, Y., Takahashi, S., Goto, C., Hashimoto, N., Hosoyamada, T., Nagao, T., Mizuno, Y., Yano, K., Nagaoka, O., Honda, S. and Tatehata, H. (1993), Tsunami Devastates Japanese Coastal Region, Eos, Trans., Am. Geophys. Union, 74, pp. 417 and 432.
Braddock, R. D. (1969), On Tsunami Propagation, J. Geophys. Res., 74, 1952-1957.
Dziewonski, A. S. (1969), A Technique for the Analysis of Transient Seismic Signals, Bull. Seism. Soc. Am., 59, 427-444.
Eckart, C., Surface waves in water of variable depth, Scripps Institution of Oceanography Wave Report 100 (1951).
Fuller, J. D. and Mysak, L. A. (1977), Edge Waves in the Presence of an Irregular Coastline, J. Phys. Ocean., 7, 846-855.
Greenspan, H. P. (1956), The Generation of Edge Waves by Moving Pressure Distributions, J. Fluid Mech., 1, 574-592.
Hammack, J. L. (1973), A Note on Tsunamis: Their Generation and Propagation in an Ocean of Uniform Depth, J. Fluid Mech., 60, 769-799.
Hatori, H., Distribution of tsunami energy on the circum-Pacific zone, In Proceedings, IUGG/IOC International Tsunami Symposium (Wakayama, Japan, 1993).
Heaton, T. H. and Hartzell, S. H. (1987), Earthquake hazards on the Cascadia Subduction Zone, Science, 236, 162, 168.
Houston, J. R. and Garcia, A. W., Type 16 Flood Insurance Study: Tsunami Predictions for the West Coaast of the Continental United States, U.S. Army Engineer Waterways Experimant Station Technical Report H-78-26 (1978).
Hwang, L.-S., Butler, H. L. and Divoky, D. J. (1972), Tsunami Model: Generation and Open-sea Characteristics, Bull. Seism. Soc. Am., 62, 1579-1596.
Kanamori, H. and Kikuchi, M. (1993), The 1992 Nicaragua Earthquake: A Slow Tsunami Earthquake Associated with Subducted Sediments, Nature, 361, 714-716.
Leblond, P. H. and Mysak, L. A., Waves in the Ocean (Elsevier Scientific Publishing Company 1978).
Mei, C. C., The Applied Dynamics of Ocean Surface Waves (John Wiley & Sons 1983).
Munk, W. H., Snodgrass, F. E. and Carrier, G. (1956), Edge Waves on the Continental Shelf, Science, 123, 127-132.
Okada, Y. (1985), Surface deformation due to Shear and Tensile Faults in a Half-Space, Bull. Seism. Soc. Am., 75, 1135-1154.
Oppenheimer, D., Beroza, G., Carver, G., Dengler, L., Eaton, L., Gee, L., González, F., Jayko, A., Li, W. H., Lisowski, M., Magee, M., Marshall, G., Murray, M., McPherson, R., Romanowicz, B., Satake, K., Simpson, R., Somerville, P., Stein, R. and Valentine, D. (1993), The Cape Mendocino, California, Earthquakes of April 1992: Subduction at the Triple Junction, Science, 261, 433-438.
Roberts, J. A. and Chien, C.-W., The Effects of Bottom Topography on the Refraction of the Tsunami of 27-28 March 1964: The Crescent City Case, Meteorology Research, Inc. Report (1964).
Satake, K. (1995), Linear and Non-linear Computations of the 1992 Nicaragua Earthquake Tsunamis, PAGEOPH, this volume.
Satake, K., Bourgeois, J., Abe, K., Abe, K., Tsuji, Y., Imamura, F., Iio, Y., Katao, H., Noguera, E. and Estrada, F. (1993), Tsunami Field Survey of the 1992 Nicaragua Earthquake, Eos, Trans., Am. Geophys. Union, pp. 74, 145 and 156-157.
Stokes, G. G. (1846), Report on Recent Researches in Hydrodynamics, 16th Meeting Brit. Assoc. Adv. Sci., 1-20.
Ursell, F. (1952), Edge Waves on a Sloping Beach, Proc. R. Soc. Lond., A, 214, 79-97.
Weaver, C. S. and Shedlock, K. M., Estimates of Seismic Source Regions from Consideration of the Earthquake Distribution and Regional Tectonics in the Pacific Northwest, U.S. Geological Survey, Open-File Report 91-441 (1992).
Whitmore, P.M. (1993), Expected Tsunami Amplitudes and Currents along the North American Coast for Cascadia Subduction Zone Earthquakes, Natural Hazards, 8, 59-73.
Wiegel, R. L. (1976); Tsunamis, in Seismic Risk and Engineering Decisions, (ed. Lomnitz, C. and Rosenblueth, E.) (Elsevier Scientific Publishing Company, Amsterdam 1976) pp. 225-286.
Wilson, B. W. and Torum, A., The Tsunami of the Alaskan Earthquake, 1964, U.S. Army Corps of Engineers Coastal Engineering Research Center Technical Memorandum 25 (1968).
Yeh, H., Imamura, F., Synolakis, C., Tsuji, Y., Liu, P. and Shi, S. (1993), The Flores Island Tsunamis, Eos, Trans., Am. Geophys. Union, pp. 74, 369 and 371-372.




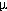 n(x,y) = A ei(kny-wnt) e-knxLn(x).
n(x,y) = A ei(kny-wnt) e-knxLn(x). r/
r/
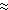 .01 appears to be a robust estimate over the first 25 km.
.01 appears to be a robust estimate over the first 25 km.
 and
and 
